TessieBoat

1. 什么是矩阵

如图，是一个表格，每个表格中，有一些数据来表示信息。如果我们把其中的数字单独提取出来，就是矩阵。

如图，我们就把上面的表格表示成了一个矩阵。

特殊定义

对于一些特殊的矩阵，有一些定义。

$\left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{matrix} \right]$

以上，就是一个方阵，就是拥有的行数和列数相等的矩阵。

$\left[ \begin{matrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \end{matrix} \right]$

以上，就是一个零矩阵，矩阵中所有的数都是0。

$\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 2 \end{matrix} \right]$

矩阵中对角线上的值都不为0的，其余都为0的，是对角矩阵。因为是对角线，所以对角矩阵一定是方阵。

$\left[ \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right]$

在对角矩阵中，如果对角线上的值都为1的，叫做单位阵。

$\left[ \begin{matrix} 5 & 0 & 0 & 0\\ 0 & 5 & 0 & 0\\ 0 & 0 & 5 & 0\\ 0 & 0 & 0 & 5 \end{matrix} \right]$

在对角矩阵中，如果对角线上的值都为一个数，叫做数量阵。

$\left[ \begin{matrix} 2 & 9 & 3 & 7 & 1\\ 0 & 3 & 6 & 4 & 1\\ 0 & 0 & 4 & 2 & 4\\ 0 & 0 & 0 & 9 & 8\\ 0 & 0 & 0 & 0 & 7 \end{matrix} \right]$

如图所示，是一个上三角阵。

$\left[ \begin{matrix} 9 & 0 & 0 & 0 & 0\\ 3 & 5 & 0 & 0 & 0\\ 1 & 5 & 3 & 0 & 0\\ 7 & 5 & 1 & 6 & 0\\ 4 & 1 & 7 & 3 & 1 \end{matrix} \right]$

这样，就是一个下三角阵。

因为有对角线的要求，所以上三角阵和下三角阵都是方阵。上三角阵和下三角阵统称为三角阵。

2. 矩阵有什么用？

肯定就会有人问了，你把数据单独提取出来，有桃子用啊。

最为简单的，就是表示方程，如图的方程

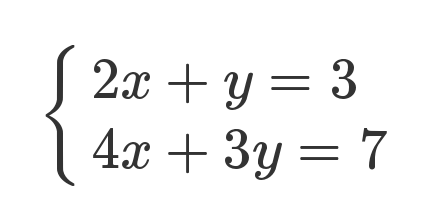
可以表示为

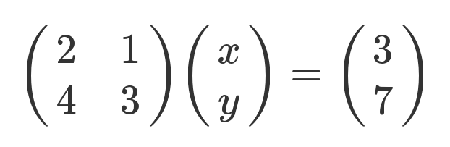
它的运算法则就很复杂了。

仔细观察会发现，结果中的第一行第一列等于左边矩阵的第一行第一列乘以右边矩阵的第一行第一列加上左边矩阵的第一行第二列乘以右边矩阵的第一行第二列。（想一想，为什么）

现在我们就可以直接进入线性方程组环节。

这样的方程，可以表示为

3. 消元过程

讲了这么多高大上的东西，是不是觉得很牛逼？

但是啊，实际上高斯消元就相当于多元一次解方程

这样的一个方程，变成矩阵，然后带入消元，跟小学生的解方程没有任何区别。

嗯，就是这样。

4. 代码实现

我当时觉得啊，高斯消元好简单啊啊啊啊，这时，同学甩过来这句话

寻思一下，还真的不好实现啊。

通过等式的乘除，进行多个等式的加减，削掉一些变量。

第一步，把方程1的x1系数a1分别化为方程2-方程n的x1系数

第二步，然后将方程2-方程n减去得到的新方程，从而消掉方程2-方程n中的x1。

第三步，接着用方程2的x2继续把方程3-方程n中的x2消掉……

第N步，……

比如，我们对于这个方程

我们首先合并①和②

2和4的最小公倍数是4，所以

然后相减，得

用同样的方法合并①和③，我们就有俩等式了

不断循环下去，我们就可以得到139z=139

所以z=1

嗯，那么，然后呢？

我们可以在存贮的时候选用二维数组，然后一个一个得覆盖，由于等式每次都会少一层，让它留在那一层，然后再反推回去就可以了。

最小公倍数的求法，我们用

int gcd(int a,int b)
{   
    if(a%b==0)  return b;
    else    return gcd(b,a%b);
}
 
int lcm(int a,int b)
{
    return a*b/gcd(a,b)  
}

由于我个人的做法是要在原数组上直接乘，为了回退，所以我又开了一个数组来存。以下是输入部分，非常简单。

int n;
scanf("%d",&n);
	
for(int i=1;i<=n;i++)
{
	  for(int j=1;j<=n+1;j++)
		{
			scanf("%d",&a[i][j]);
			c[i][j]=a[i][j];
		}
}

以下对于解方程的代码，不懂的可以看看注释掉的内容，或者自己研究一下。i用于循环1-n的变量的循环。为什么是n-1呢？是因为那时候直接求结果就ok啦！

	for(int i=1;i<=n-1;i++)
	{
		//printf("现在我们来消除x%d\n",i);
		for(int op=1;op<=n-i;op++)
		{
			int bei1=1,bei2=1;
			if(a[i][i]<0)
			{
				bei1=-1;
				a[i][i]*=-1;
			}
			if(a[i+op][i]<0)
			{
				bei1=-1;
				a[i+op][i]*=-1;
			}
			
			
			int o=lcm(a[i][i],a[i+op][i]);
			bei1=bei1*o/a[i][i];
			bei2=bei2*o/a[i+op][i];
			//printf("目前在计算第%d行和%d行  bei1:%d   bei2:%d\n",i,i+op,bei1,bei2);
			
			
			a[i+1][i]=0;
			for(int j=i+1;j<=n+1;j++)
			{
				c[i][j]=a[i][j]*bei1;
				c[i+op][j]=a[i+op][j]*bei2;
				//int oo=a[i+op][j];//
				
				a[i+op][j]=c[i][j]-c[i+op][j];
				//printf("a[%d][%d]的%d-a[%d][%d]的%d=%d \n",i,j,a[i][j],i+op,j,oo,a[i+op][j]);
			}
			//printf("\n");	
		}
	}

这里我们需要注意的是，如果你要通分的系数正好是负数，要取相反数。

这样子，我们只是制成了一个新的矩阵，求解还要一段代码。

	for(int i=n;i>=1;i--)
	{
		for(int j=n;j>=i+1;j--)
		{
			a[i][n+1]-=a[i][j]*b[j];
		} 
		b[i]=a[i][n+1]/a[i][i];
	}

当然，它非常简单。

5. 其余问题

我在学习这个当中，发现有的博客有使用单位阵来解释的，表示最后的解，我觉得也是一种挺好的方法。

6. 源代码

#include <stdio.h>
int a[104][104];
int b[104];
int c[104][104];
int gcd(int o,int oo)
{   
    if(o%oo==0)  return oo;
    else    return gcd(oo,o%oo);
}
 
int lcm(int o,int oo)
{
    return o*oo/gcd(o,oo);    
    
}
 
int main()
{
	int n;
	scanf("%d",&n);
	
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n+1;j++)
		{
			scanf("%d",&a[i][j]);
			c[i][j]=a[i][j];
		}
	}
	
	
	for(int i=1;i<=n-1;i++)
	{
		//printf("现在我们来消除x%d\n",i);
		for(int op=1;op<=n-i;op++)
		{
			int bei1=1,bei2=1;
			if(a[i][i]<0)
			{
				bei1=-1;
				a[i][i]*=-1;
			}
			if(a[i+op][i]<0)
			{
				bei1=-1;
				a[i+op][i]*=-1;
			}
			
			
			int o=lcm(a[i][i],a[i+op][i]);
			bei1=bei1*o/a[i][i];
			bei2=bei2*o/a[i+op][i];
			//printf("目前在计算第%d行和%d行  bei1:%d   bei2:%d\n",i,i+op,bei1,bei2);
			
			
			a[i+1][i]=0;
			for(int j=i+1;j<=n+1;j++)
			{
				c[i][j]=a[i][j]*bei1;
				c[i+op][j]=a[i+op][j]*bei2;
				//int oo=a[i+op][j];//
				
				a[i+op][j]=c[i][j]-c[i+op][j];
				//printf("a[%d][%d]的%d-a[%d][%d]的%d=%d \n",i,j,a[i][j],i+op,j,oo,a[i+op][j]);
			}
			//printf("\n");	
		}
	}
	//printf("---------------------------\n");
	/*
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n+1;j++)
		{
			printf("%d ",a[i][j]);
		}
		printf("\n");
	}*/
	
	for(int i=n;i>=1;i--)
	{
		for(int j=n;j>=i+1;j--)
		{
			a[i][n+1]-=a[i][j]*b[j];
		} 
		b[i]=a[i][n+1]/a[i][i];
	}
	
	for(int i=1;i<=n;i++)
	{
		printf("x%d:%d\n",i,b[i]);
	}
	
	return 0;
}

如有需要，请开大数组。

输入格式为先输入n，然后输入这个二维矩阵。

好了，就到此结束啦！

这是我目前写过的最长的博客