一个改编的故事

年轻的泰勒同学在做数学计算时遇到了问题：一些可以无限求导的函数，比如三角函数的代值计算，简直不是人算的。但是为了解决自己眼下的计算难题，泰勒想出来的一个对策：能不能找到一个相似又好算的函数，如果精准度足够，就能应付了事。

一个相似的函数需要具备什么？需要在初始点上值相同，在这个点上导数相同，在这个点上凹凸性相同，还要在这个点上导数的凹凸性相同……

来帮帮忙！

好，那么假设现在泰勒把寻找相似函数的任务交给了你。（什么李华行为）让我们现在来寻找一个函数，让它能满足泰勒对于$\cos{x}$的近似计算。

为了方便，我们直接选择从$x=0$这个点进行拟合：首先时初始点上的值相同，这个都知道是$y=1$。然后是导数相同，这个你也该知道是 $y^\prime=0$。满足这两点非常简单，只需要一个直线就能满足：

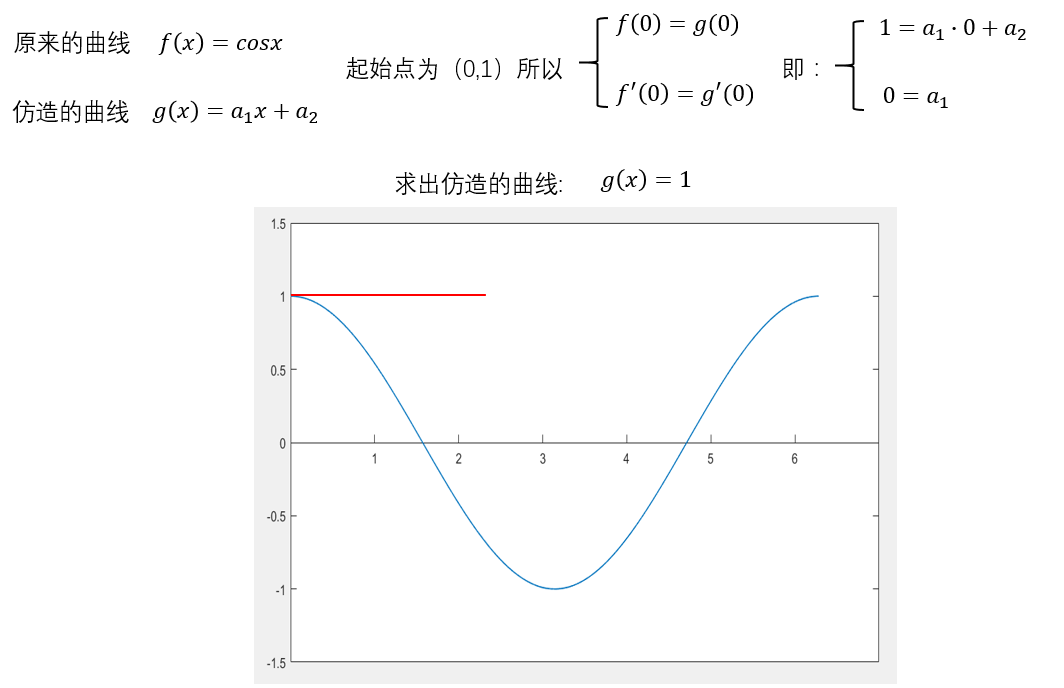
让我们来进行第二步，来满足这里的凹凸性相同。凹凸性可以用导数的导数表示。为什么这样讲？导数的导数大于0时候，代表导数向上穿过$x$轴，说明函数先减后增，是凹型；导数的导数小于0时候，就是凸型。这一步也很简单，一个二次函数就能满足：

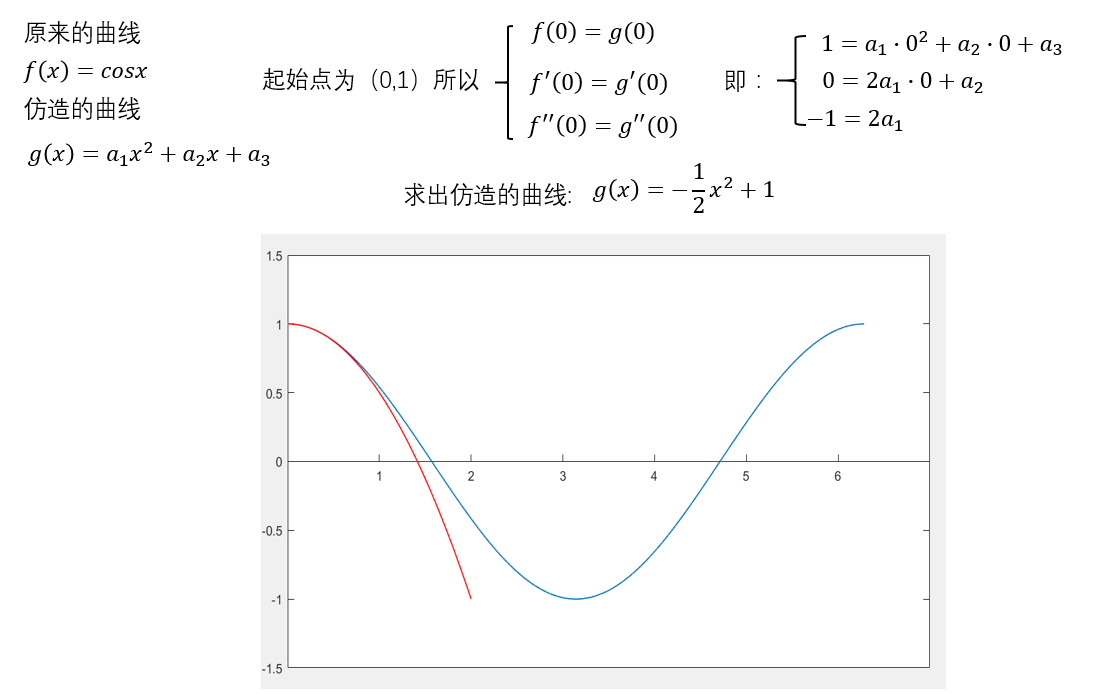
或许你现在应该知道下一步是什么了，满足导数的凹凸性相同，即导数的导数的导数，然后是导数的导数的导数的导数……

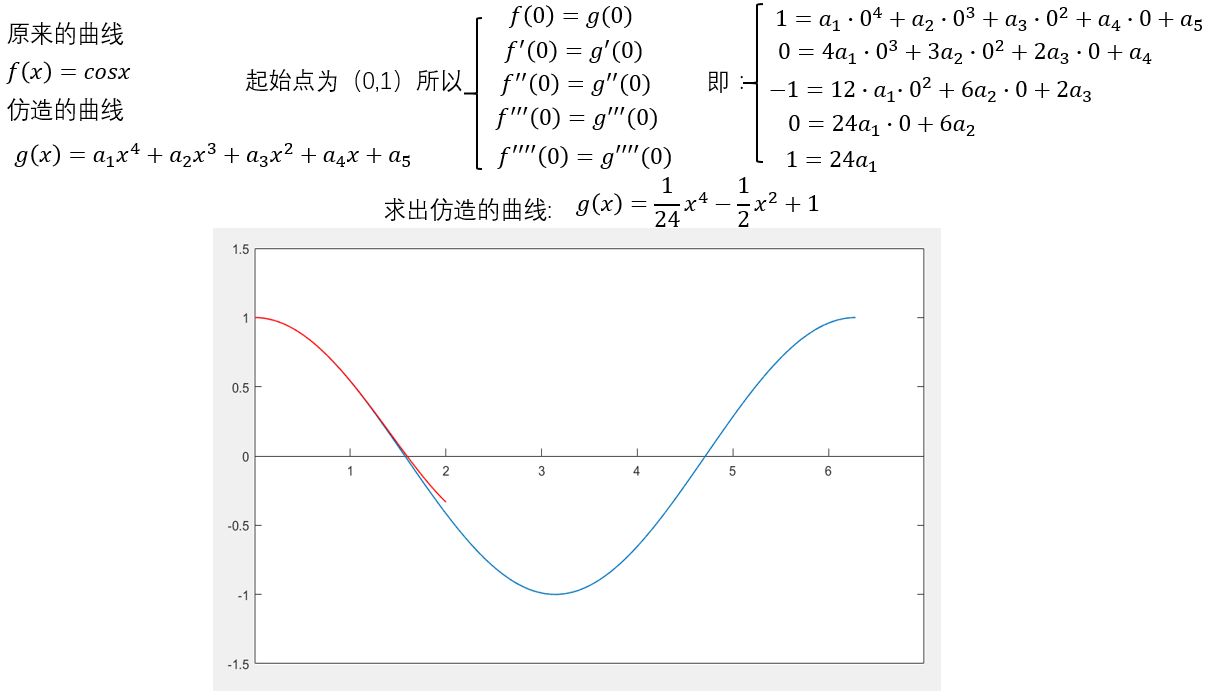
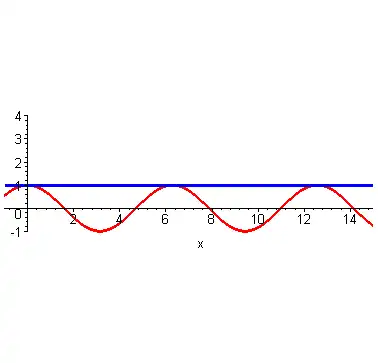
一步一步重复，通过增加更高次的项，你会发现这个函数越来约接近$\cos{x}$了！

好耶，我们完成了任务！用一张动图来展现一下我们逐渐拟合的过程吧：

用数学公式表达

我们已经用一个情景展现了泰勒展开的过程。现在让我们用数学语言来表达一下。

首先，我们用多项式进行拟合，需要的最后结果是这个形式：

$g(x)=a_{0}+a_{1} x+a_{2} x^{2}+\ldots \ldots+a_{n} x^{n}$

拟合的第一步是在$x=x_0$时值相等：

$g\left(x_0\right)=f\left(x_0\right)=a_0$

然后，我们需要让从$1$到$n$次的导数都相等：

$g^{n}(x_0)=f^{n}(x_0)$

这其实是比较好算的，为了让多次求导相等，我们可以算出$a_n$的值为：

$a_{n}=\frac{f^{n}(x_0)}{n !}$

非常简单！那么我们最后拟合出来的函数是：

$g(x)=g\left(x_{0}\right)+\frac{f^{1}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{2}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\ldots \ldots+\frac{f^{n}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}$

故事好像没有结束

还记得开始的描述吗？我们的目的是找到一个精准度足够的拟合函数。我们拟合出来的函数偏究竟差了多少，我们应该怎么计算偏差来判断拟合出的函数误差是否超过了需要的精准度？

佩亚诺余项

现在我们知道了，如果拟合的进程趋近于无限，那么我们就认为拟合出了完全相同的函数。那么，没有添加的高次项，就是我们的误差（假设我们拟合到$n$次）：

$f\left(x\right)-g\left(x\right)=\frac{f^{\left(n+1\right)}\left(x_0\right)}{\left(n+1\right)!}\left(x-x_0\right)^{n+1}+\cdots+\frac{f^{\left(\infty\right)}\left(x_0\right)}{\infty!}\left(x-x_0\right)^\infty$

回顾一下我们的拟合过程：用越来越小的高次项对函数进行贴合，添加的每一项都越来越小。

想到这个，佩亚诺于是认为：当误差小于原函数的最小项（即最后一项），就认为可以忽略这个误差。

怎么比较大小呢？这里最好用的是除法，因为同时包含了$x+x_0$的$n$次方，可以约掉。两个式子相除，整理一下，我们得到了：

$\frac{f\left(x\right)-g\left(x\right)}{f\left(x\right)_{min}}=\frac{f^{\left(n+1\right)}\left(x_0\right)}{\left(n+1\right)f^{\left(n\right)}\left(x_0\right)}\left(x-x_0\right)+\frac{f^{\left(n+2\right)}\left(x_0\right)}{\left(n+1\right)\left(n+2\right)f^{\left(n\right)}\left(x_0\right)}\left(x-x_0\right)^2+\cdots$

猜猜为什么佩亚诺为什么放在这节的首位？因为他扔出来这个式子结果发现自己不会算。但为了收个场，最后佩亚诺还是给出了一个结论，就是当$x$趋近于$x_0$时，算出来的商趋近于$0$，认为误差可以忽略。

拉格朗日中值定理

这不是糊弄人吗？对于我们前面的$\cos{x}$，甚至我们拟合出来的直线$y=1$也满足这个情况，但是这个直线很明显完全无法解决我们需要的近似计算的问题。佩亚诺相当于只是把问题细化了，然后丢了出去。

下一位接手这个问题的人，是拉格朗日。

这是一个小学生都懂的常识：对于一段路程，汽车驶过的平均速度是$v$。如果汽车在过程中有一个时刻小于$v$，那就必定有一个时刻速度大于$v$，反之亦然。而在这个速度的变化过程中，也必定有时刻汽车的速度恰好等于平均速度$v$。

用数学语言表达，就是：对于函数$f\left(x\right)$，如果在范围$\left[x_1,x_2\right]$内连续且可导，那么必定存在$x=a$满足:

$f^\prime\left(a\right)=\frac{f\left(x_1\right)-f\left(x_2\right)}{x_1-x_2}$

这个定理，被称作拉格朗日中值定理。

柯西中值定理

柯西：好东西，我的。柯西发现这里的$x$也可以替换成一个函数，对于函数$f\left(x\right)$和函数$g\left(x\right)$，如果都在在范围$\left[x_1,x_2\right]$内连续且可导，那么必定存在$x=a$满足:

$\frac{f^\prime\left(a\right)}{g^\prime\left(a\right)}=\frac{f\left(x_1\right)-f\left(x_2\right)}{g\left(x_1\right)-g\left(x_2\right)}$

拉格朗日余项

接下来，拉格朗日着手于处理泰勒展开的误差问题。

首先，我们把误差项设为$R\left(x\right)=f\left(x\right)-g\left(x\right)$。前面我们已经发现了，误差项由两坨组成，而包含了$x+x_0$的项更加容易处理一些，我们单独提出来令$T\left(x\right)=\left(x-x_0\right)^{n+1}$。

$R\left(x\right)$除以$T\left(x\right)$，我们添加两个明显等于$0$的项，得到：

$\frac{R(x)}{T(x)}=\frac{R(x)-0}{T(x)-0}=\frac{R(x)-R\left(x_{0}\right)}{T(x)-T\left(x_{0}\right)}$

这东西好熟悉……这不就是柯西中值定理吗？依葫芦画瓢，我们一定可以找到一个值$\xi$，满足：

$\frac{R\left(x\right)}{T\left(x\right)}=\frac{R\left(x\right)-R\left(x_0\right)}{T\left(x\right)-T\left(x_0\right)}=\frac{R^\prime\left(\xi\right)}{T^\prime\left(\xi\right)}=\frac{R^\prime\left(\xi\right)}{\left(n+1\right)\left(\xi-x_0\right)^n}$

让我们来看分子，是计算$R\left(x\right)$的导数：

$R^\prime\left(x\right)=\left(n+1\right)\frac{f^{\left(n+1\right)}\left(x_0\right)}{\left(n+1\right)!}\left(x-x_0\right)^n+\left(n+2\right)\frac{f^{\left(n+2\right)}\left(x_0\right)}{\left(n+2\right)!}\left(x-x_0\right)^{n+1}+\cdots$

可以发现，$R^\prime\left(x_0\right)=0$。

让我们来看分母，可以发现$x=x_0$时，分母也是0。那么很巧妙的，我们又可以构造出一个柯西中值定理。
让我们令分子$R^\prime\left(\xi\right)=P\left(\xi\right)$，分母$\left(n+1\right)\left(\xi-x_0\right)^n=Q\left(\xi\right)$：

$\frac{R^{\prime}\left(\xi\right)}{(n+1)\left(\xi-x_{0}\right)^{n}}=\frac{P\left(\xi\right)}{Q\left(\xi\right)}=\frac{P\left(\xi\right)-0}{Q\left(\xi\right)-0}=\frac{P\left(\xi\right)-P\left(x_{0}\right)}{Q\left(\xi\right)-Q\left(x_{0}\right)}=\frac{P^{\prime}\left(\xi_{2}\right)}{Q^{\prime}\left(\xi_{2}\right)}$

嗷，这个过程其实是可以一直重复下去的，和泰特展开式一样。

重复进行无数次后，可以得到：

$R\left(x\right)=\frac{f^{n+1}(a)}{(n+1) !}\left(x-x_{0}\right)^{n+1}$

ヽ(✿ﾟ▽ﾟ)ノ好耶，我们发现我们已经将无数多的误差项整合成了一项！

现在，只需要带入点$x=a$，就可以得到我们需要的误差值来进行判断了！

故事的终点

模仿，重复，嵌套……最终，我们用泰勒的方法解决了泰勒的问题。

不过其实，抛弃掉拉格朗日的思路，我们有一条捷径来通往这个看起来很复杂的答案。

回到我们的第一步，原函数$f\left(x\right)$等于拟合函数$g\left(x\right)$加误差$R\left(x\right)$。我们对等式$n$次求导后，拟合出来的函数$g\left(x\right)$就只剩一项$g^{\left(n\right)}\left(x\right)$了。很明显，$g^{(n)}\left(x\right)=f^{\left(n\right)}\left(x_0\right)$。所以我们得到了等式：

$f^{\left(n\right)}\left(x\right)-f^{\left(n\right)}\left(x_0\right)=R^{\left(n\right)}\left(x\right)$

无从下手？别忘了拉格朗日中值定理：一定存在一个值$a$属于$\left[x,x_0\right]$，满足了这两点之间的“平均速度”。即用$f^{\left(n+1\right)}\left(a\right)\cdot\left(x-x_0\right)$替换掉$f^{\left(n\right)}\left(x\right)-f^{\left(n\right)}\left(x_0\right)$，于是我们得到了：

$R^{\left(n\right)}\left(x\right)=f^{\left(n+1\right)}\left(a\right)\cdot\left(x-x_0\right)$

求导$n$次，就是：

$R\left(x\right)=\frac{f^{n+1}(a)}{(n+1) !}\left(x-x_{0}\right)^{n+1}$

与上面的一模一样！大功告成！