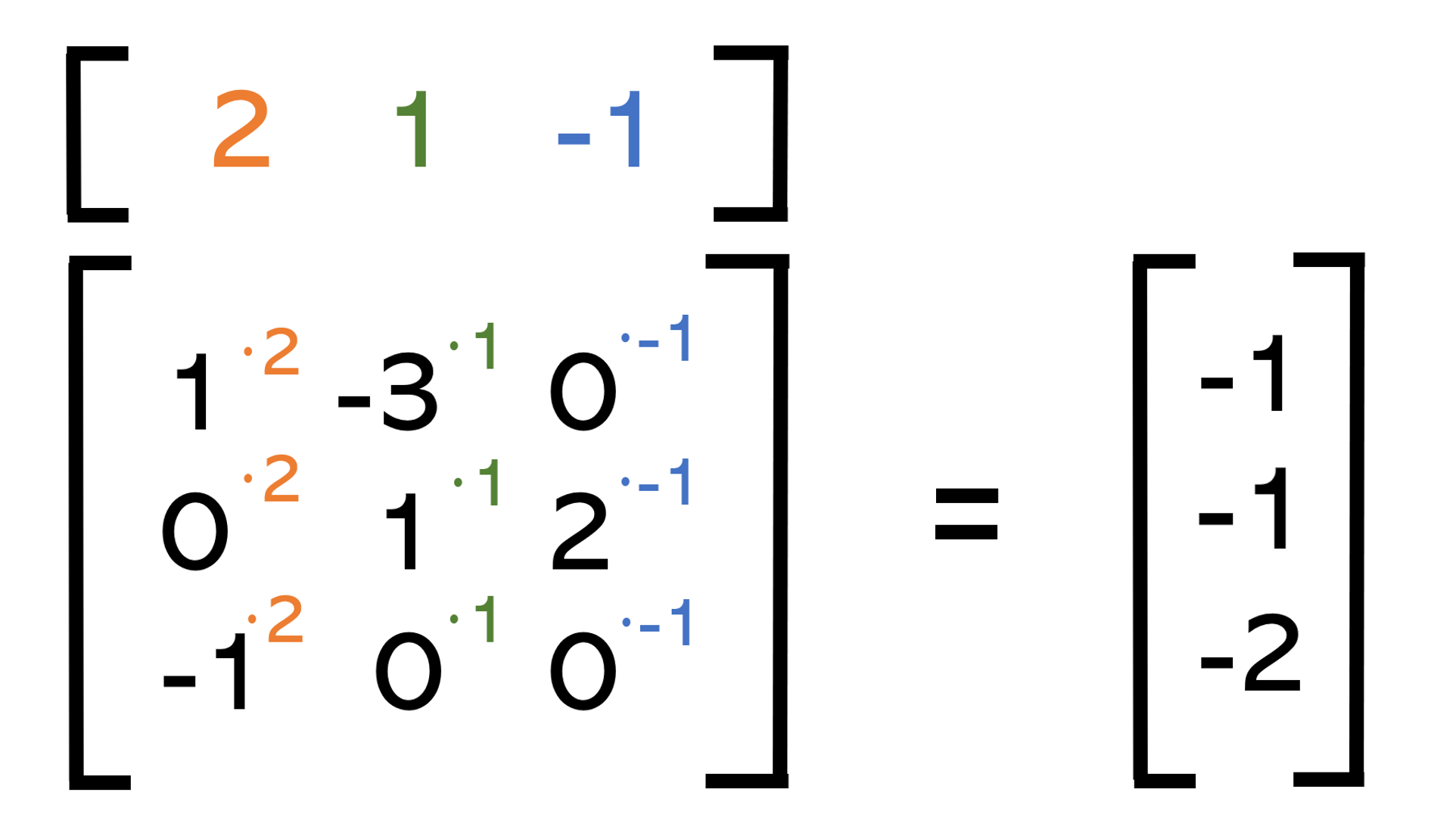等等等等等一下！仅仅包含数字的表格，凭什么可以相乘？即使可以相乘，它们相乘要由什么规则来运算呢？

操作向量的工具

还记得吗？我们在开头丢出了一句话：矩阵是操作向量的工具。而在众多对于矩阵乘法的解释中，这是最直观，也最直白的。不如我们就用上面用过的基向量来举例吧：

$\ a=\ \left[\begin{matrix}1\\0\\\end{matrix}\right] b=\ \left[\begin{matrix}0\\1\\\end{matrix}\right]$

比如我们想要生成一个向量$\ \left[\begin{matrix}3\\-2\\\end{matrix}\right]$，我们需要将向量$a$翻3倍，向量$b$乘上-2倍，就能组成这个向量。而用矩阵乘法，就是这样表示的：

$\ \left[\begin{matrix}1&0\\0&1\\\end{matrix}\right]\times\left[\begin{matrix}3\\-2\\\end{matrix}\right]=\left[\begin{matrix}3\\-2\\\end{matrix}\right]$

通过调整后面$1\times 2$的矩阵，就可以操作前面两个向量的倍率，生成二维空间内的任意向量。

而当向量$a$和$b$发生变化时，可以看作是线性得扭曲了坐标轴，导致了最终结果的变化。

矩阵乘法

唔，以此类推，我们可以写出三维，四维，以及更高维度的向量操作，但这并不包含了所有的矩阵乘法。对于更普适的矩阵乘法，是怎么表达的呢？

我们不如动态得描述一下我们在上面是怎么进行乘法运算的。为了具体一点，我们就举个例子吧，我们目前有三个向量：

$\ a=\ \left[\begin{matrix}1\\0\\-1\\\end{matrix}\right] b=\ \left[\begin{matrix}-3\\1\\0\\\end{matrix}\right] c=\ \left[\begin{matrix}0\\2\\0\\\end{matrix}\right]$

然后我们把向量拼在一起，形成一个大矩阵：

$\left[\begin{matrix}1&-3&0\\0&1&2\\-1&0&0\\\end{matrix}\right]$

然后，我们需要将向量$a$乘上2倍，$b$向量乘上1倍，$c$向量乘上-1倍来生成向量：

$\left[\begin{matrix}1&-3&0\\0&1&2\\-1&0&0\\\end{matrix}\right]\times\left[\begin{matrix}2\\1\\-1\\\end{matrix}\right]=?$

别急，因为你不看这个式子不会矩阵乘法也会算，所以——别真的先将向量$a$乘上2倍，$b$向量乘上1倍，$c$向量乘上-1倍，然后加起来，不然讲这么多就浪费力。

我们的第一步是算$x$的坐标值，也就是第一行：

$1\times 2+(-3)\times 1+0\times 2=-1$

然后是$y$的坐标值，也是第二行：

$0\times 2+1\times 1+2\times (-1)=-1$

最后是$z$的坐标值，也是第三行：

$(-1)\times 2+0\times 1+0\times 2=-2$

发现规律了吗？直接的说，就是将第二个矩阵转90°扣到了前面矩阵的头上：

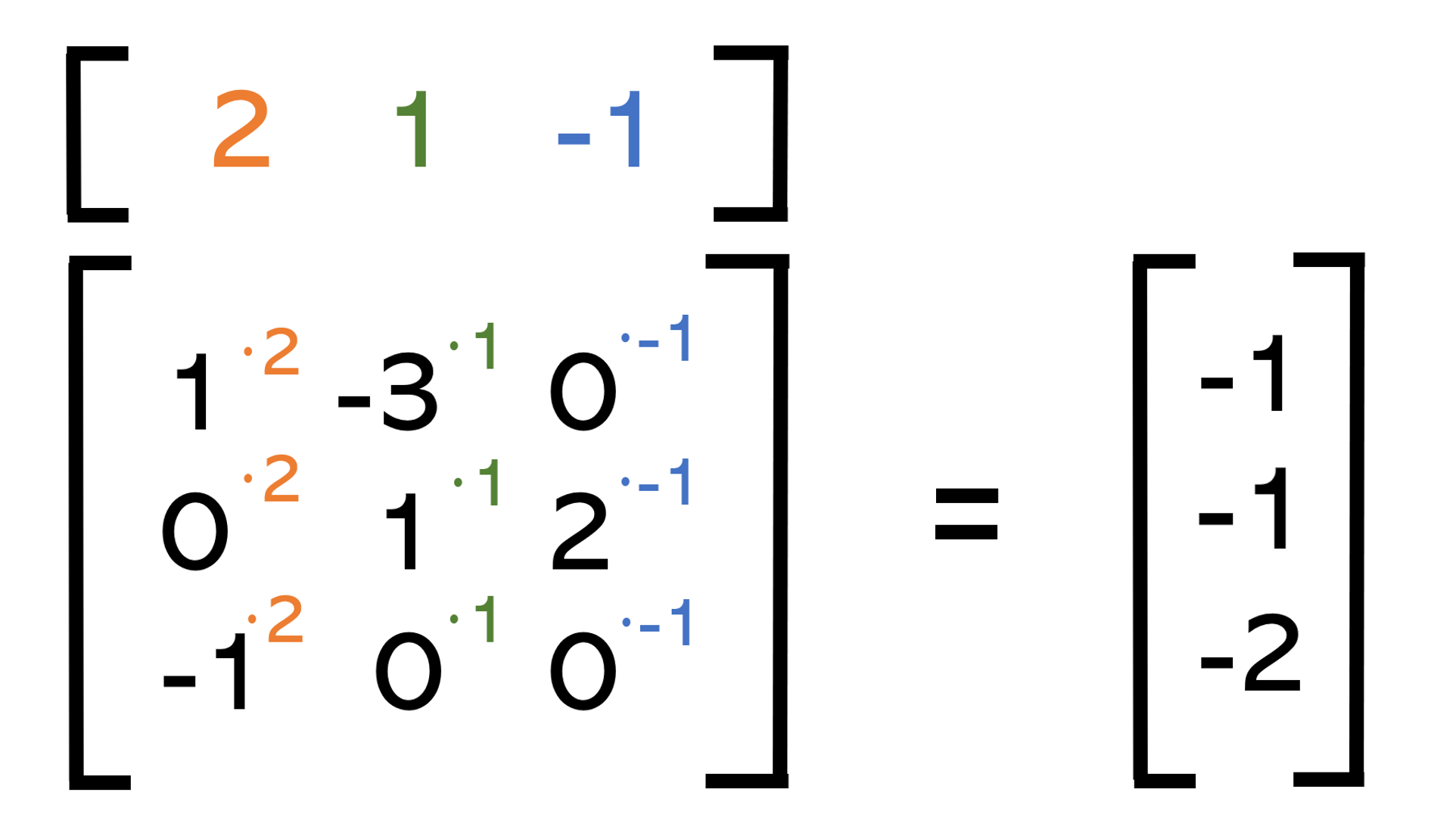
如果这个时候第二个矩阵有两列，然后就是按顺序扣第一行和第二行，算出来的两个数值分别为同行的第一个的数字和第二个数字。

对了，别忘了：如果矩阵想要相乘，第一个矩阵的列数必须等于第二个矩阵的行数。（如果不等，扣过来就对不齐了）

运算法则

顺序性

矩阵乘法拥有顺序性，乘法的两边不能调换顺序：

$A\times B \cancel{=} B\times A$

结合律

矩阵乘法满足结合律，乘法运算先后可以调换。

$(A\times B)\times C=A\times(B\times C)$

分配律

矩阵乘法满足分配律，可以拆开括号。

$A\times\left(B+C\right)=A\times B+A\times C$

转置矩阵

表示为$A^T$，意思是将矩阵按从左上到右下的对角线进行翻折，即：

$a_{i,j}=a_{j,i}^\prime$

分块的矩阵乘法

对矩阵进行分块，计算完结果之后再带入，不会影响计算结果。所以你甚至可以这样切：

$\left[\begin{array}{ccc|c} 5 & 0 & 3 & 6\\ 3 & 1 & 2 & 5\\ 4 & 1 & 8 & 9\\ \hline 6 & 7 & 5 & 2\\ \end{array}\right]= \left[\begin{array}{c|c} A_1 & A_2\\ \hline A_3 & A_4\\ \end{array}\right]$

其他规则

矩阵翻转两次，就是矩阵自身：

$\left(A^T\right)^T=A$

矩阵乘上单位矩阵就是自身，反之亦然：

$A\times I=A\\ I\times A=A$