故事重提

相信你和我一样，高中的物理知识已经忘完了，那我们就从最简单的开始：

牛顿三大定律

牛顿第一定律（惯性定律）：一个物体在不受力（或合力为0）的情况下，总是保持静止或匀速直线运动。

牛顿第二定律（加速度定律）：对一个物体施加力，物体获得的加速度与其质量成反比，加速度与力的方向相同。

$\vec{F}=m\vec{a}=\frac{d\vec{p}}{dt}$

力也是动量$\vec{p}$的变化率，牛顿单位是$kg\cdot m/s^2$。

牛顿第三定律（后坐力定律）：作用力与反作用力大小相同，方向相反。

$\vec{N}=-\vec{F}$

移动与能量

相信你已经注意到了，我们现在在大学部份将更严谨得展现公式与单位之间的关系，也将我们曾经的公式引入向量概念，以达到更加完美的量纲分析。

比如，我们曾经定义力做功$W=F\cdot L$，那么，在位移与力都具有向量特征时，正确的表达应该是这样：

$W=\int_{a}^{b}{\vec{F}d \: \vec{l}}$

这个也很好理解，就是积移动的每一段微分，而不是我们在高中一味追求的直线运动。

要说能量之前，我们把力分为两种，一种是可以进行能量储存（势能）和消耗的力，叫做保守力；作为及时产生于消耗的力，叫做非保守力。比如，弹力就是一种保守力，摩擦力就是一种非保守力。

关于重力：

$\vec{G}=m\vec{g}\qquad W_G=mgh$

关于弹力：

$\vec{F}=-k\vec{x}\qquad W_F=\frac{1}{2}kx^2$

关于动能：

$E_k=\frac{1}{2}mv^2$

动量与碰撞

在前面我们提到，动量$\vec{p}=m\vec{v}$。每一次物体的碰撞或者粘连，即使能量丢失，都一定满足动量守能：

$m_A\vec{V_A}+m_B\vec{V_B}=m_A\vec{V_B'}+m_b\vec{V_B'}$

对于没有机械能损失的碰撞，叫做弹性碰撞，反之则叫非弹性碰撞。特别的，两个黏在一起，是能量损失最多的，被叫做完全非弹性碰撞。

丢一个弹性碰撞的公式在这里，免得以后现场推（1号碰静置的2号）：

$v_1^\prime=\frac{m_1-m_2}{m_1+m_2}\cdot v_1\\ \text{ }\\ v_2^\prime=\frac{2m_1}{m_1+m_2}\cdot v_1$

需要注意的是，多个物体碰撞之后进入了不同的方向，向量中的速度乘以质量同样满足动量守恒。

质心

一个物体的质心是这个物体的理想质量中心点，在均匀受力时，可以假象为质点受力。经过微积分的学习，现在我们可以精确得表达质心（我们假设一个o点作为起点参考点，p点为质心，总质量为M）：

$\vec{r_{op}}=\frac{1}{M}\int\vec{r}dm$

如果想要在现实中找到重心，可以两次挂着作垂线，用相交得出的重心位置来找到质心。

天体与旋转

在圆周运动中，我们要将力分解为维持转动半径的向心力和提供角速度的力。

天体运动作为高中物理的一个大重点，相信这个看一眼就够了：

$F=G\frac{M\cdot\ m}{r^2}=m\omega^2r=m\frac{v^2}{r}=m\frac{4\pi^2}{T^2}r$

以上是高中的公式，有几个特殊的点需要提及：

第一是高中的这些公式依旧是不带有方向的，为了保证拥有向量特征的表达，需要在公式中增加$\frac{\vec{r}}{\left|\vec{r}\right|}$增加方向性的表达，比如我们的引力公式就变成了：

$\vec{F}=G\frac{M\cdot\ m}{\left|\vec{r}\right|^3}\cdot \vec{r}$

第二是我们需要重新说明角速度的方向。角速度$\vec{\omega}$包含了角速度大小，也包含了顺时针/逆时针的方向关系。这与右手螺旋定理相似，四指的方向是转动方向，大拇指朝向的就是角速度的方向。所以，角速度的方向和转动的平面垂直。

转动惯量

直觉告诉我们，在一个转盘的中间给一个力和在转盘的外围给一个力，效果是不一样的。这来自杠杆原理：力矩的差异导致了不同的效果。（这里需要注意的是，力矩不是杠杆的长度，而是长度乘以力的大小，即$\vec{\tau}=\vec{l}\times \vec{F}$）

关于转动时候的能量，我们可以把一个转动的物体想象成一个在等效半径上转动的一个点，这样我们就能用$E_k=\frac{1}{2}mv^2$来表示转动的能量。其中，$v=\omega \cdot r$，带入进去得到$E=\frac{1}{2}m{(\omega \cdot r)}^2$。为了与动能的公式达到形式上的相等，我们定义出一个转动时的质量，叫做转动惯量$I=m\cdot r^2$:

$E_v=\frac{1}{2}mv^2 \qquad E_\omega=\frac{1}{2}I\omega^2$

我们曾经学过，一个物体的惯性只与质量有关。在转动的中，转动的惯性与质量的分布有关。

在转动中，我们将角速度的加速度名作$\alpha$，为了在牛顿第二定理上的一致，我们可以将力替换成力矩以保证单位多出来的长度满足等式：

$\vec{F}=m\vec{a} \qquad \vec{\tau}=I\vec{\alpha}$

关于转动惯量中的等效半径，可以参考教材上的这个表：（从应试的角度来说，背下来就行了）

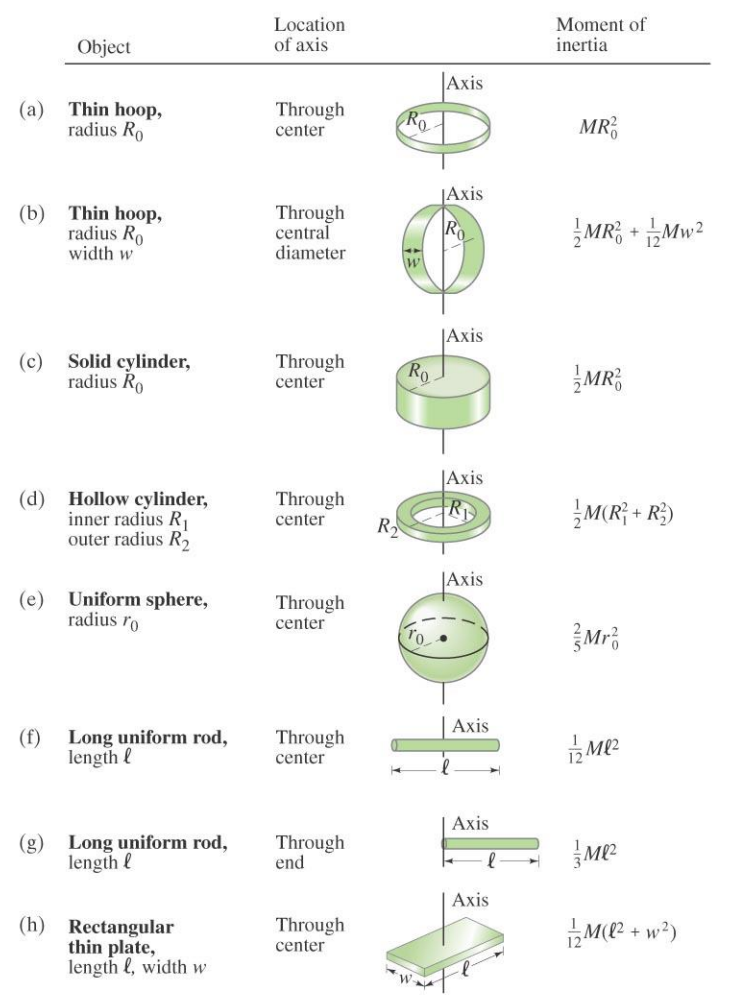
这其实很好理解，对于一个质量均匀的圆盘，等效半径是$r=\frac{\sqrt{2}}{2}R$；对于一个圆环，等效半径是$r=\frac{\sqrt{2({R_1}^2+{R_2}^2)}}{2}$。

更加严谨的表达，是这个：

$I=\int{R^2}dm$

什么意思呢，就是积每一个质量小块的$m\cdot r^2$，用它证明以上公式需要一定数学功底，这里就先不讲了。或许等我哪天闲得要命就来更新一下？

转动惯量还满足两个规律：

第一个是当物体沿着质心轴转动，转动轴平移$l$长度的话，之后的转动惯量只需要加上$m\cdot l^2$即可：

$I^{\prime}=I+m\cdot l^2$

第二个是关于互相垂直的轴，穿过质心转动物体，两个之和等于第三个：（以x,y,z轴为例子）

$I_x+I_y=I_z$

或许你已经发现了，我们提到的力矩的等式是现在第一次使用叉叉的乘号而不是点号表示乘以。如果你不知道这两个的区别，可以去看看我们的《矩阵：神奇的数字表格》。大致来说，用叉叉计算两个向量，得到的向量会垂直于这两个向量所在的平面，向量的长度等于这两个向量组成的平行四边形的面积。

叉乘的绝妙程度在于，你可以不需要将力分成向心力和转动力，让计算更加简便化，也可以更方便得处理顺时针和逆时针的问题。

弹簧与震动

对于弹簧，我们在高中学过$F=kx$，如果把弹簧末端挂根笔，让纸平移：

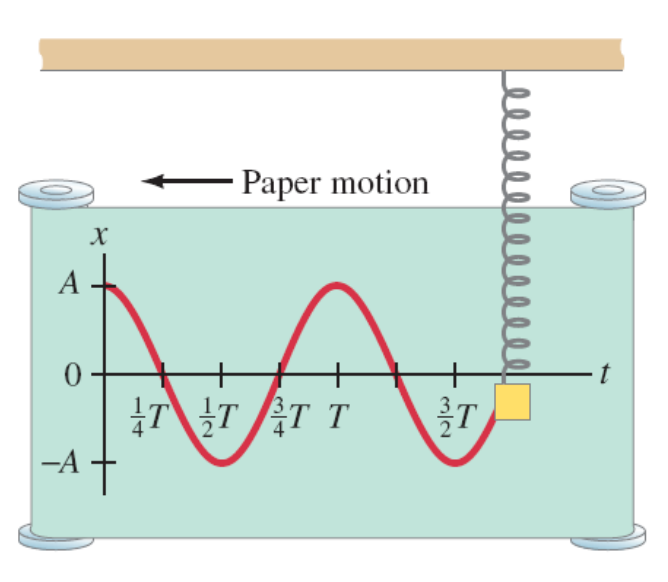
我们可以用三角函数来表达这个图象：

$x=A\cos{\left(\omega t+\phi\right)}$

这个图像的一些等式相信老师也教过：

$v=\frac{dx}{dt}=-\omega A\cos{\left(\omega t+\phi\right)}\\ f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}\quad T=2\pi\sqrt{\frac{m}{k}}$

对于同样是周期性运动的单摆来说，$F\approx-\frac{mg}{L}x$，相当于$k=\frac{mg}{L}$，直接把上面的等式替换一下就行：

$f=\frac{1}{2\pi}\sqrt{\frac{g}{L}}\quad T=2\pi\sqrt{\frac{L}{g}}$

关于共振叠加，横波纵波的概念很简单，看名字应该就等于复习了，这里就跳过了。

再温电学