矩阵的秩

我们曾经一直使用“矩阵的有效列”来规避矩阵中可以被其他向量生成的向量。对于一个矩阵的有效列数量，我们可以使用秩$rank(A)$来表示。

如何计算一个矩阵的秩呢？要是你已经看完了前面的所有的笔记，相信基本都已经会计算矩阵的秩了。不过如果你要是完全不会，看了笔记还是不会，我建议你可以看看这个长长脑子。

为了这篇文章看起来长一点，所以我们还是举个例子来说明一下，比如计算这个矩阵的有效列数：

$\left [ \begin{matrix} -2&-1&-1&1&2\\ 1&1&-2&1&4\\ 4&-6&2&-2&4\\ 3&6&-9&7&9 \end{matrix} \right ]$

我们使用行变换，将矩阵变成类似高斯消元的形式：

$\left [ \begin{matrix} 1&0&-1&0&4\\ 0&1&-1&0&3\\ 0&0&0&1&-3\\ 0&0&0&0&0 \end{matrix} \right ]$

好的，我们可以看到第一、二、四列是基本列，所以这个矩阵的秩为3。

矩阵的特征值

一个矩阵的特征值($eigenvalue$)，就是在计算矩阵乘法$A\cdot x$中，可以替代矩阵$A$的数值$\lambda$，就像这样：$A\cdot x=\lambda x$。使用$(A-\lambda I)x=0$计算。

其中，$|A-\lambda I|$被称作特征多项式，计算出来是一个包含$\lambda$的多项式函数，令它等于0，就可以解出$\lambda$的值。（一般都有多个解）

比如计算下面这个矩阵的特征值：

$\left [ \begin{matrix} -1&1&0\\ -4&3&0\\ 1&0&2 \end{matrix} \right ]$

我们需要计算特征多项式：

$|A-\lambda I|= \left | \begin{matrix} -1-\lambda&1&0\\ -4&3-\lambda&0\\ 1&0&2-\lambda \end{matrix} \right | =0$

计算的结果是：

$(2-\lambda)(\lambda-1^2)=0$

我们得到，这个矩阵的特征值$\lambda$为1或2。

对矩阵进行操作，特征值会造成同等计算规则的影响。比如$A$的特征值是$\lambda$，$A^2$的特征值就是$\lambda^2$，$A^-1$的特征值就是$\lambda^-1$，$A^2+A$的特征值就是$\lambda^2+\lambda$。需要注意的是，转置矩阵特征值不变，即$A$与$A^T$的特征值都是$\lambda$。

两个生成一个

基础铺垫完成，我们现在将来介绍叉积($cross\ product$)——由两个三位向量生成特征向量的运算，使用$\nu=a\times b$表示。生成的特征向量，将可以代替这两个向量，作为体积计算的简化步骤。

生成的特征向量垂直于两个向量的平面，长度等于它们所围成的平行四边形的面积。

为什么这样做呢？先想想我们是怎么计算体积的：$V=S\times h$，底乘高，非常简单。

现在我们已经选了两个向量并算出来它们的底面积了，那么我们只需要知道第三个向量投影出来的高就可以啦，即$h=l_3\cdot \cos{\theta}$。

这里我们需要计算$\nu\cdot l_3$就能得到体积了，因为$\nu$的长度为$S$，即$\nu\cdot l_3=S\cdot l_3\cdot \cos{\theta}=S\times h=V$：

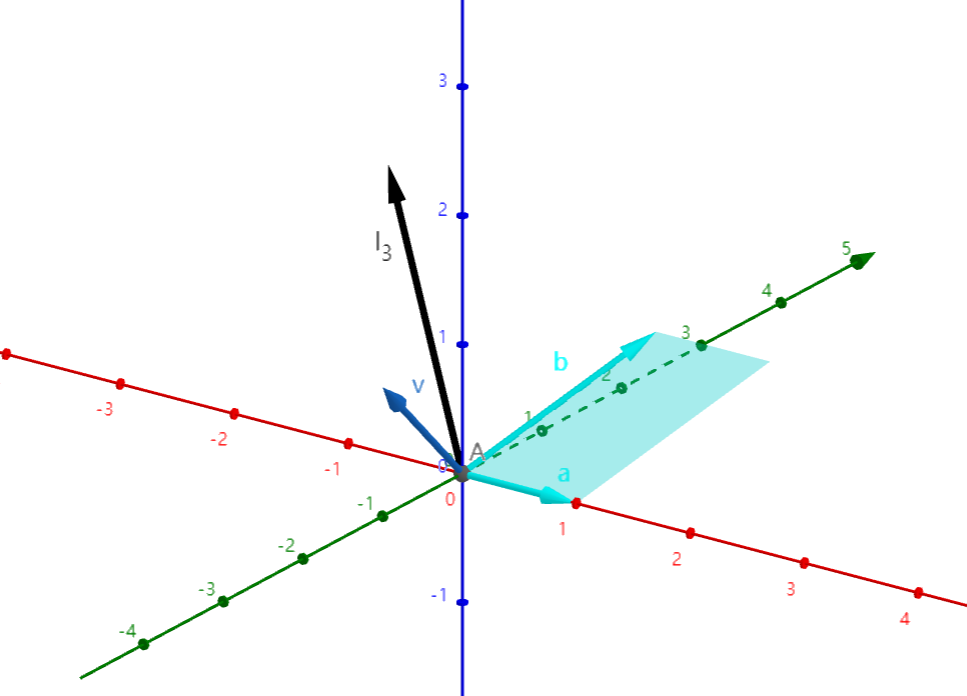
我们如何计算叉积

如果有一定数学直觉，相信你在这里已经知道叉积是如何计算的了。比如，让我们求这两个向量的叉积：

$\ v_1=\ \left[\begin{matrix}1\\-2\\-1\\\end{matrix}\right],v_2=\ \left[\begin{matrix}-2\\4\\1\\\end{matrix}\right]$

那我们先假设第三个向量是$\left[\begin{matrix}a\\b\\c\\\end{matrix}\right]$。如果我们计算这个六面体的体积，最简单的方式是使用行列式：

$V=\left | \begin{matrix} a&1&-2\\ b&-2&4\\ c&-1&1 \end{matrix} \right | =2a+b+0c$

上面我们定义了，我们的结果$V=v_3\cdot (v_1 \times v_2)$。那么，我们可以很轻易的得到，我们的特征向量为：$v_1 \times v_2=\left[\begin{matrix}2\\1\\0\\\end{matrix}\right]$。

通过叉积生成的向量的方向，满足右手法则。则中指为第一个向量，食指为第二个向量，则大拇指为特征向量的方向。就像这样：

严格规定方向的原因，是这里行列式计算出来的"体积"，包含负数的可能。

再谈行列式

我们曾经在行列式章节提到，二阶行列式表示两个向量生成的平行四边形的面积。唔，真的是这样吗？比如，你来计算一下这两个二维向量围成的平行四边形的面积：

$\ a=\ \left[\begin{matrix}1\\1\\\end{matrix}\right],b=\ \left[\begin{matrix}3\\0\\\end{matrix}\right]$

这不简单嘛……你看，我们只要计算行列式，就可以得到答案为3——

$S= \left | \begin{matrix} 1&1\\ 3&0 \end{matrix} \right | =0-3=-3$

答案……是$-3$？

我们的答案变成负数了，这是怎么回事？

当然，你可以说行列式交换任意一组行列会导致结果变号。但这其实是在回避这个问题的几何本质——比如我们再来问一句，为什么行列式交换了就会导致变号？

在行列式章节中，我们讲过，变号的几何本质是空间的翻面。但这里我们只给出了两个向量，谈何翻面呢？所以，让我们来重新开始讲讲——

我们的二维空间由$x$轴与$y$轴生成，并令单位长度为$1$，其中，每个由$x$轴一个与$y$轴一格围成的面积为$1$：

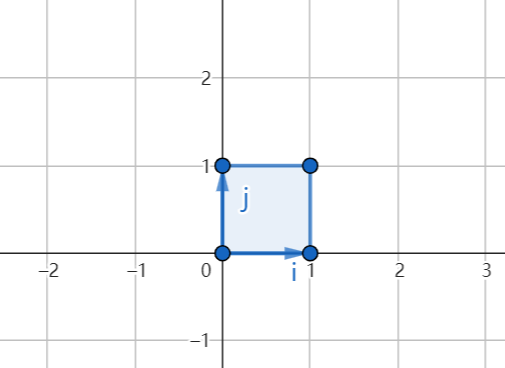
我们所有的向量，都是由两个基底生成。亦或者说，我们的两个向量，就是扭曲了这个空间，比如我们将$x$轴翻倍，此时面积就变为了$2$：

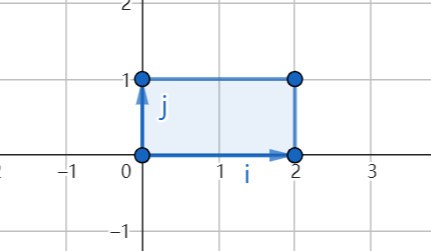
而我们上面计算的面积，就是让$x$轴的基底，变成了上面的$\left[\begin{matrix}1\\1\\\end{matrix}\right]$，而$y$轴的基底移到下面，变成了$\left[\begin{matrix}0\\3\\\end{matrix}\right]$。

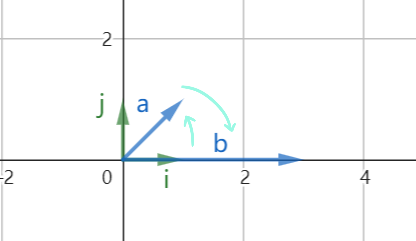
两个坐标轴在线性变换中交叉了，移到了对方的一侧，在变换中，造成了空间的翻面。

所以我们需要严格规定顺序，即行列式计算面积时，第一个向量与第二个向量逆时针排列时（第一个向量在右侧时），行列式结果为正值，反之则为负值。

放到三维中也一样，为了保证保证行列式结果的一致性，我们也需要规定这个“垂直于两个向量”的特征向量的方向，即右手法则。

叉积的运算法则

反交换律：$a\times b=-b\times a$

分配律：$a\times(b+c)=a\times b+a\times c$

拉格朗日公式

他的名字你应该不陌生，我们在《关于泰勒展开》章节中有提到过拉格朗日中值定理，为我们解决余项的大小问题推进了一步。现在又是把他叫出来的时候啦！当我们面对连续的三重矢积时，可以使用以下的拉格朗日公式：

$(a\times b)\times c=b(a\cdot c)-a(b\cdot c)\\ a\times (b\times c)=b(a\cdot c)-c(a\cdot b)$

同时，这里还有一个拉格朗日恒等式：

$(a\times b)\cdot(c\times d)=(a\cdot c)(b\cdot d)-(a\cdot d)(b\cdot c)$

二维和三维的暴力证明非常简单，你只需要设坐标然后拆开就能完成证明。要谈几何上的证明，比如第一个式子，$a\times b$垂直于$a$与$b$构成的平面，那么$a\times b$与$c$构成的平面必定与$a$与$b$构成的平面垂直（一个平面内有一条直线垂直于另一个平面，则这两个平面垂直）。由于我们都将原点视为向量起点，所以我们的三重矢积的结果向量也会在$a$与$b$构成的平面上，可以直接由$a$与$b$生成。

这非常难以理解！在探寻三重矢积几何意义的时候，new Bing给出的一个错误的说法激起了我的灵感。如果将$a,b,c$放入行列式，是否可以凑出我们需要的答案呢？

经过尝试，我们发现这个想法是可行的，如果你用行列式的第一列进行计算：

$(a\times b)\times c=- \left | \begin{matrix} a&a&0\\ b&b&0\\ c&0&c \end{matrix} \right | \\ \qquad \\ a\times (b\times c)=- \left | \begin{matrix} a&0&a\\ b&b&0\\ c&c&0 \end{matrix} \right |$

在括号内的第三个数字是0，在括号外的第二个数字是0，非常简单。不过，如果你用第一行计算立马就露馅了。由于点积不是乘法，不满足交换律，你会得出错误的答案。

结语

毫不夸张的说，叉积的内容是我上大学目前期间最不能接受的教学。普通的教学方式是先将叉积结论给出，直接在学生完全不知道$a,b,c$是什么意思的情况下得出叉积结果，在教学上直接回避体积问题，而将叉积当作新概念来教学，求体积只是一道例题。

我们的pearson的多元微积分教材更进一步，直接把上学期一整学期都把向量竖着放在行列式的习惯舍弃（教材全篇没有专门讲横着和竖着排一样），将$\left|\begin{matrix}a&b&c\\\end{matrix}\right|$放在第三行，更是加大了学生的理解难度。

所以我一直讲，我很佩服我们的教材与老师将问题复杂化的能力。或许纯正的概念是数学理论的基石，不过在数学的教学上，我更希望将问题具象话、简单化。复杂的过程就先别提公式，带着学生走一遍；复杂的概念就别故弄玄虚，用学生熟悉的东西开始讲起。

或许，等到我们教学的“唯结果论”结束时，这份数学的简单与有趣就会真正的呈现在每个学生的面前。