再识偏导数

如果你看过我们之前的章节《关于隐函数的求导》，介于某些高级教材的原因，我们已经提前知道了偏导数$\partial$代表分子的扰动有多大程度得影响分母。

我们需要补充的是，几何上三维曲面$f(x,y)=z$，它的$\frac{\partial y}{\partial z}$，相当于用平面$y=y_0$切这个曲面，这个二维图像上$x=x_0$的导数，也被写作$f_y(x,y)$。

链式法则

在高中我们就已经学过嵌套函数$g(f(x))$的求导，两次求导就是分别求$x$→$f(x)$→$g(f(x))$的两次变换分别会对结果造成多少倍的影响，将它们相乘就是我们的结果，用偏导数写就是这样：

$\frac{\partial x}{\partial g(f(x))}=\frac{\partial f(x)}{\partial g(f(x))}\cdot \frac{\partial x}{\partial f(x)}$

而比如$x,y$可以由关于$t$的参数方程表示，而且$f(x,y)=z$，那么如果我们求$\frac{\partial t}{\partial z}$时，也可以使用链式法则：各变量对结果造成的扰动加起来等于最终造成的扰动：

$\frac{\partial t}{\partial z}=\frac{\partial x}{\partial z}\cdot \frac{\partial t}{\partial x}+\frac{\partial y}{\partial z}\cdot \frac{\partial t}{\partial y}$

三维中的极值点

像我们学习二维的函数一样，我们现在需要了解三维中的极值点应该怎样判断。理所当然的，我们知道这里关于$x$和$y$的偏导都为0：$f_x(x,y)=f_y(x,y)=0$。而为了更加深一步的判断，我们就需要二阶偏导，相当于与$x-z$和$y-z$平面切线的凹凸性。

蒋蒋！让我们隆重介绍——黑塞矩阵($Hessian\ matrix$):

$H(x,y)=\left[\begin{matrix}f_{xx}\left(x,y\right)&f_{xy}\left(x,y\right)\\f_{yx}\left(x,y\right)&f_{yy}\left(x,y\right)\\\end{matrix}\right]$

这个矩阵常用于使用牛顿-拉夫逊迭代法($Newton-Raphson\ method$)近似求解方程。不过这里我们只用得到它行列式的值，即:

$D(x,y)=det(H(x,y))=f_{xx}\left(x,y\right)f_{yy}\left(x,y\right)-f_{xy}\left(x,y\right)^2$

你可以把它当作二次函数的判别式$\Delta$差不多的东西，下面是它的四种情况：

当$D(x,y)>0$，且$f_{xx}\left(x,y\right)>0$，那么这个点是极小值。
当$D(x,y)>0$，且$f_{xx}\left(x,y\right)<0$，那么这个点是极大值。
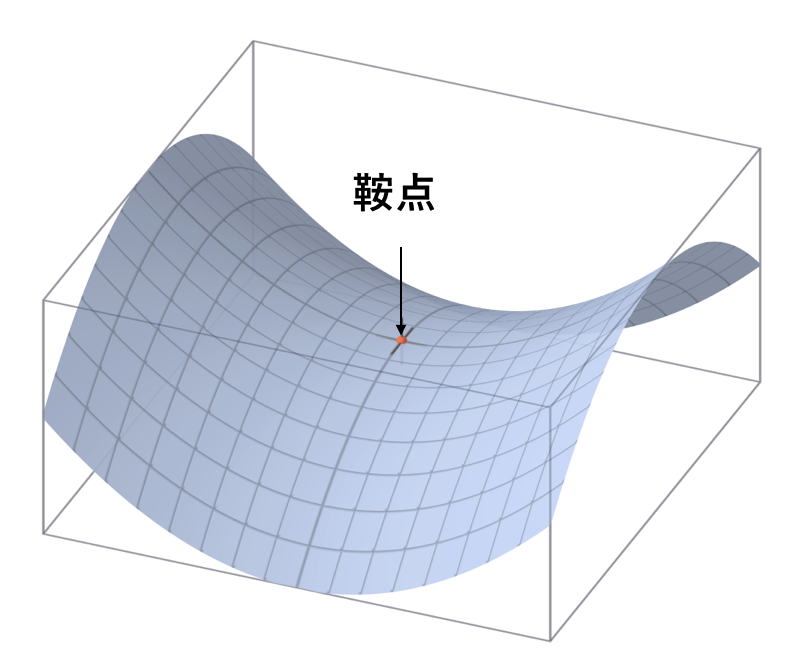
当$D(x,y)<0$，那么这个点是鞍点。
当$D(x,y)=0$，这个点可能是上面三种情况的任意一个。（无法判断）

鞍点是什么？它在一边是极大值，一边是极小值，所以啥也不是，具体长这样：

接下来我们要讲解如何求限定条件下的最值，不过我们还需要一点铺垫。

方向导数

偏导是与坐标轴构成的平面的导数，那么如果我要沿着$y=x$这个平面切曲线的导数呢？其实并不是无从下手，就是有一点麻烦，比如我们让求点$(a,b,f(a,b))$对$(\cos{\theta},\sin{\theta})$方向的导数。与我们刚刚学导数一样，我们让$t$趋近于0：

$\lim\limits_{t\rightarrow 0}{\frac{f\left(a+t\cos{\theta},b+\sin{\theta}\right)-f\left(a,b\right)}{t}}$

这里我们需要作一点特殊的处理，让两边多出来一项$f\left(a,b+\sin{\theta}\right)$，一边只有$x$变，一边只有$y$变，方便我们改写成链式法则的一部分：

$\lim\limits_{t\rightarrow0}{\frac{f\left(a+t\cos{\theta},b+\sin{\theta}\right)-f\left(a,b+\sin{\theta}\right)}{t}}+\lim\limits_{t\rightarrow0}{\frac{f\left(a,b+\sin{\theta}\right)-f\left(a,b\right)}{t}}$

改写成链式法则：

$\frac{\partial f(a,b)}{\partial x}\cdot \frac{\partial x}{\partial t}+\frac{\partial f(a,b)}{\partial y}\cdot \frac{\partial y}{\partial t}$

于是我们就得到了这个方向导数的值：

$f_x(a,b)\cdot \cos{\theta}+f_y(a,b)\cdot \sin{\theta}$

这个形式蛮简单的，相当于我们的方向$(\cos{\theta},\sin{\theta})$点乘另一个二维向量$(f_x,f_y)$。

梯度

初中生就该知道，两个向量点乘结果最大。所以当方向与这个二维向量一致时，方向导数最大。这个方向，被叫做梯度，即$\nabla f=(f_x,f_y)$。方向导数最大的值，就是梯度的长度。

作为一个形象的比喻，就是如果我在这个曲面放一个小球，它一定会顺着梯度这个方向往下滚。（这是一个拥有陷阱的比喻，因为梯度是二维向量，所以准确的说是小球是在梯度所在的平面里往下滚）

需要区分的是此时这个点切面的法向量，结果与梯度极其相似。要计算这个法向量，我们可以用平面$x=x_0$和$y=y_0$来切这个曲面，得到向量$a=(x_0,y,f(x_0,y))$与$b=(x,y_0,f(x,y_0))$，叉积之后就是我们的结果：

$-a\times b=(f_x(x_0,y_0),f_y(x_0,y_0),-1)$

之所以前面加个符号，是因为混淆性很强，这个形式与梯度非常相似。不过，你也可以理解为四维平面$f(x,y)-z=0$求出的三维梯度。

拉格朗日乘子法

基础铺垫完成！接下来我们要讲解如何寻找在限定条件下的三维最低点。我们已知的条件由一个需要求极值的曲面$f(x,y)=M$与限定条件$g(x,y)=0$组成。

这个最低点满足什么条件呢？当原曲面最大下降的方向与限制条件最快趋于满足的方向平行时（即$\nabla f=\lambda \nabla g$时），这个点就是极值点。因为如果任意移动，都会导致限制条件偏离而不满足等式或者因为不够高效得满足条件导致原函数较大而不是最低点。这里的倍数关系$\lambda$，被称作拉格朗日乘子。

很难理解？不如我们用一个教材中的例子看看——这里是一个类圆锥的曲面与一个平面相切，求这个切曲线的最底点，为了方便，我们就用等高线代替圆锥的画图：

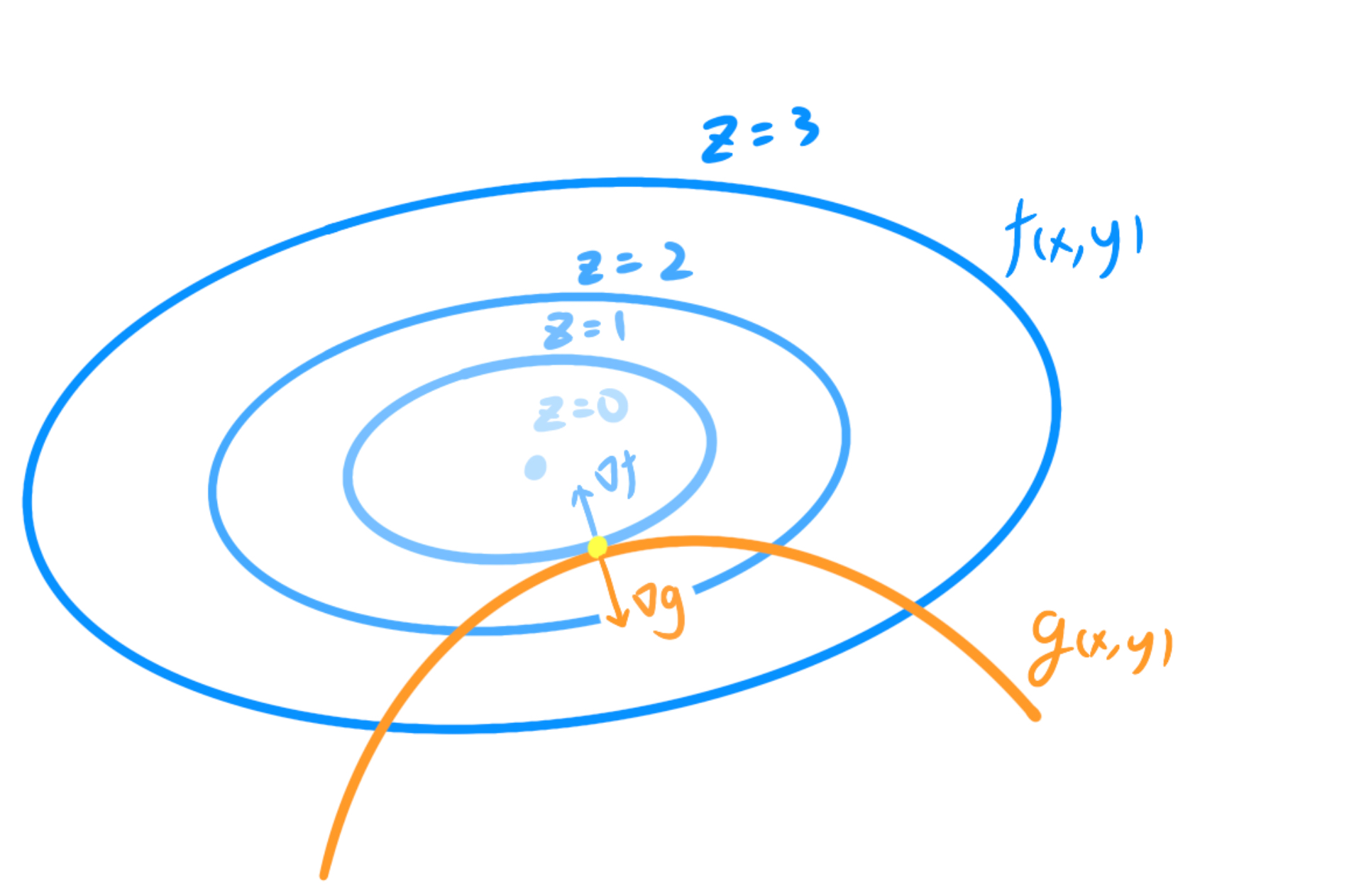
此时图中最低点很明显为$z=1$。如果不是很理解的话，你可以尝试在橙色线上移动，会发现两个梯度会有一个指向真正最低点的倾向。

如果是做题，这个等式的利用需要联立这三个方程：

$\begin{cases} \nabla f_x(a,b)+\lambda \nabla g_x(a,b)=0\\ \nabla f_y(a,b)+\lambda \nabla g_y(a,b)=0\\ g(a,b)=0 \end{cases}$

梯度下降

在卷积网络的机器学习中，我们需要机器自动调整权重$W$与偏移$b$来增加模型的正确率。所以，机器需要知道一个数值，得知他们在调整每个$w_n$或者$b_n$之后的正确率会怎么变化，来选择自己的调整策略。衡量正确率的方法，是这个简单的方差，被称作损失函数：

$Cost=\frac{1}{2N}\sum\left|Y-y\right|^2$

这样，机器就有了一个明确的目标，即让损失函数越小越好。

那怎么移动到最低点呢？最笨的方法是沿着梯度一点点往下走：

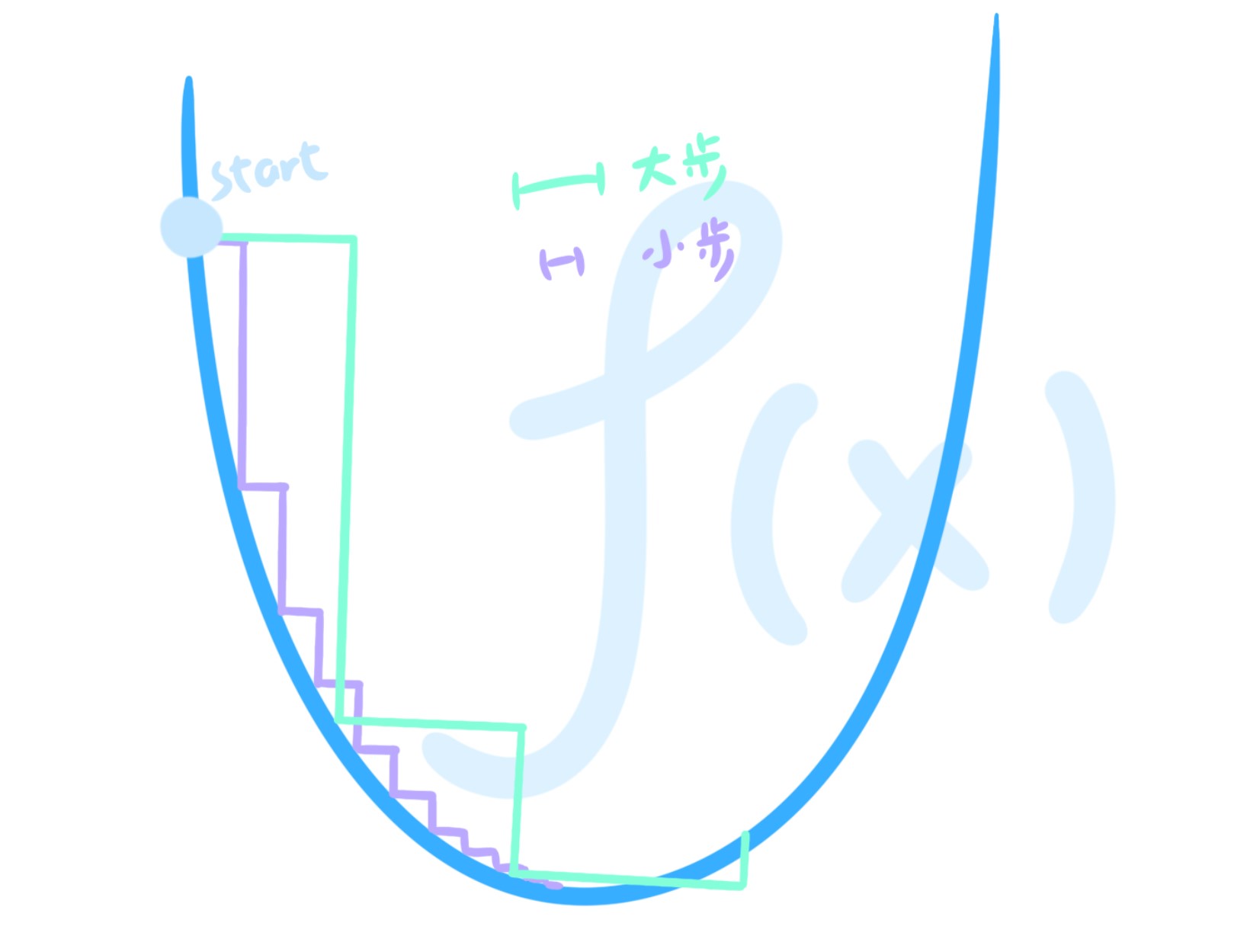
这明显不行——步伐太小会导致运行很慢，步伐太大又会绕过最优点。

聪明的办法是让移动的距离与导数成正比——在陡坡快速下移，在平缓的地方小心检查：

但理想状况终归是理想状况，比如如果这个比例太大,也会导致走出了最佳点;这个比例太小，也会导致运行过慢。而这里的步长比例，被称作学习率，需要模型训练者自己考虑。

1847年法国数学家奥古斯丁·路易·柯西，不会想到自己为了解决冗长的天体轨道方程，发明的梯度下降法让神经网络在无论多少参数，多少层，都能不断迭代，最终找到误差最低的最优解。

梯度消失与梯度爆炸

在机器模型的训练中，你可能会发现前面层数的参数几乎没动，这可能就是遇到了梯度消失现象。造成这种现象的原因是因为每一层在计算时都会乘上激活函数的偏导，而多次激活函数趋于0的偏导相乘，让结果指数级的接近0。（反之，则是激活函数过大导致前面层的参数指数级增加，被称作梯度爆炸）

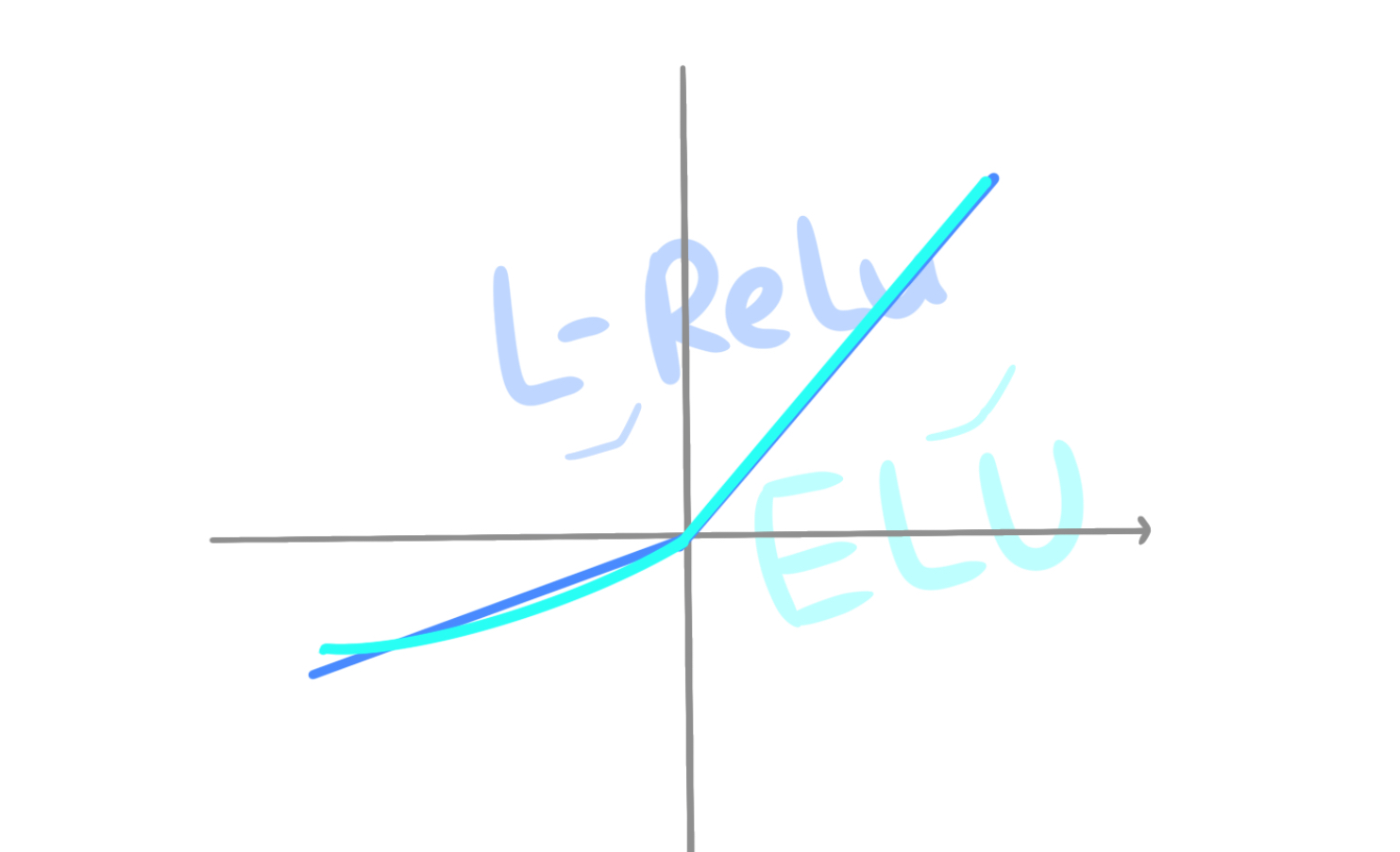
而线性整流函数($ReLU$)却独树一帜：因为0之后求导都是1，不会导致这个问题。

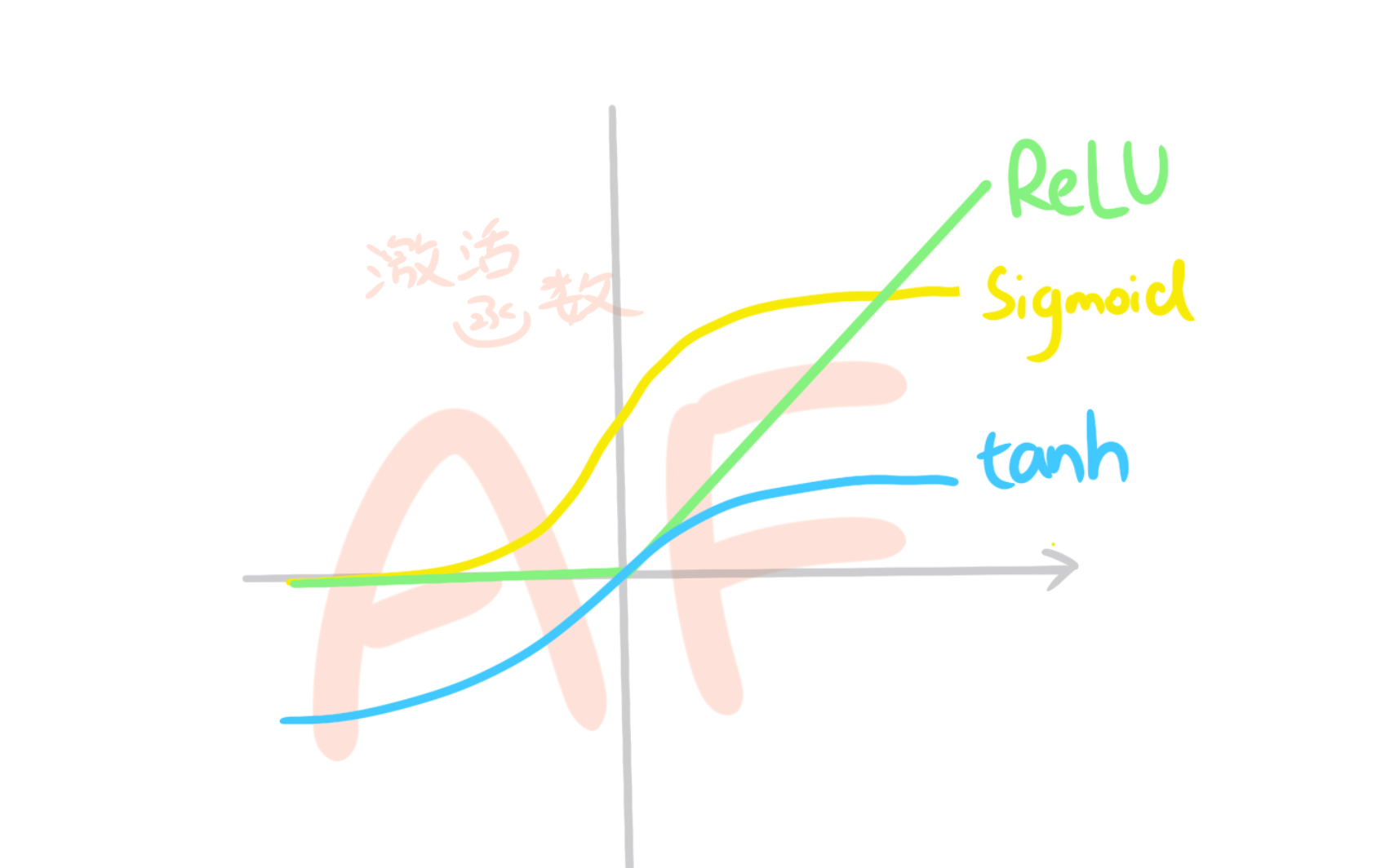
不过线性整流函数的缺点也很明显：负数部分都为0，机器就不会学习；而整数部分都为线性，只能进行线性变换，无法柔性扭曲空间，无法得到优质模型。所以，你或许可以试试这两个激活函数来解决这个问题：