接下来，让我们重磅介绍：方块矩阵的标量体积——行列式。它不仅被用于计算面积与线性变化对最终结果的影响倍率，也可以用于确定线性方程组解的个数以及形式，甚至也可以计算逆矩阵。这么厉害的东西，你一定已经迫不及待得想学了吧

算算面积

让我们来算算这个由向量$a$和$b$生成的平行四边形的面积~

$\ a=\ \left[\begin{matrix}3\\0\\\end{matrix}\right],b=\ \left[\begin{matrix}1\\1\\\end{matrix}\right]$

就像这样：

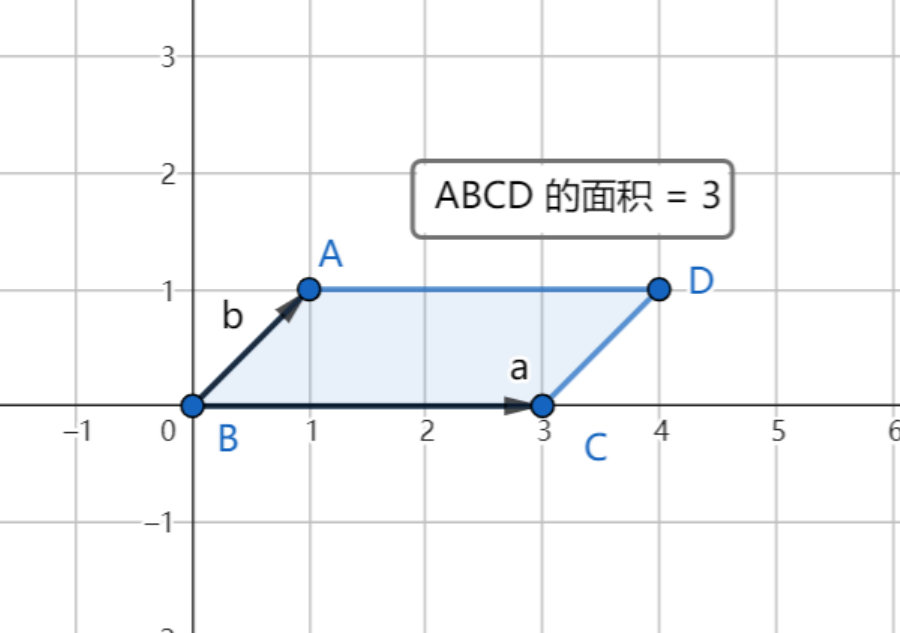
很简单，面积$S$等于底乘高，也就是$S=3\times 1=3$。

好，让我们把这个问题一般化，就像这样：

$\ a=\ \left[\begin{matrix}x_1\\y_1\\\end{matrix}\right],b=\ \left[\begin{matrix}x_2\\y_2\\\end{matrix}\right]$

无从下手？这张图能帮你理清思路：

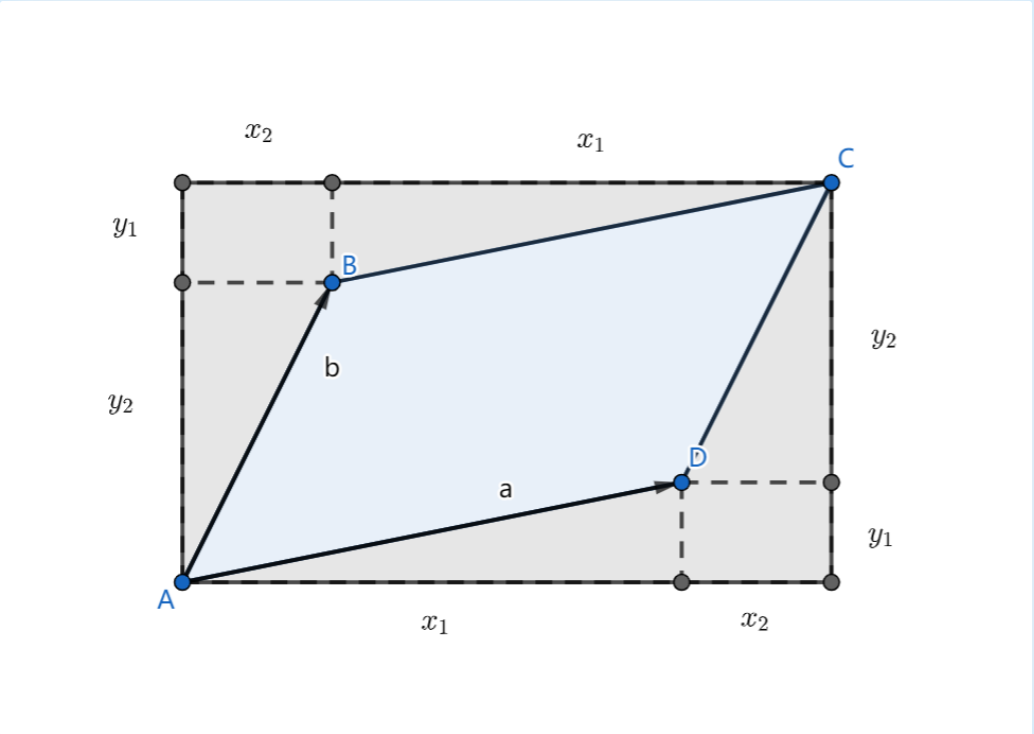
首先，大长方形的蓝色面积是$(x_1+x_2)\cdot (y_1+y_2)$，需要减去部分的灰色面积是$2x_2\cdot y_1+x_1\cdot y_1+x_2\cdot y_2$，那么蓝色部分减去灰色部分的面积就是我们要求的$S$，即$S=x_1\cdot y_2-x_2\cdot y_1$。

二阶行列式

上面的式子用行列式表示，就是正对角线的乘积减去反对角线的乘积：

$S=\left|\begin{matrix}x_1&x_2\\y_1&y_2\\\end{matrix}\right|=x_1\cdot y_2-x_2\cdot y_1$

计算行列式，可以用$det(A)$或者$|A|$表示。

这个$2\times 2$矩阵的行列式，被称作二阶行列式，表示这两个向量生成的平行四边形的面积。（不过需要注意的是，这里的“面积”也有可能是负数值，这与向量的顺序有关）

以此类推，那么三阶行列式就是表示三个向量生成的平行六面体的体积，甚至还可以计算更高的维度……

多维下的行列式

在$n$维的下的行列式计算，遵循下面这个规则：

$det(A)=\sum_{i=1}^{n}{\left(-1\right)^{1+i}\cdot\ a_{1,i}\cdot\ det(A_{1i})}$

看不懂？没关系，我们举个例子来说明一下。比如，计算下面这个三阶行列式：

$\left | \begin{matrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{matrix} \right |$

提前说明，对于公式中的$A_{1i}$，表示矩阵A中去掉第i行，第j列的部分。比如在我们现在计算行列式，需要现在这三个矩阵：

$A_{11}=\left[\begin{matrix}4&-1\\-2&0\\\end{matrix}\right], A_{12}=\left[\begin{matrix}2&-1\\0&0\\\end{matrix}\right], A_{13}=\left[\begin{matrix}2&4\\0&-2\\\end{matrix}\right]$

通过计算，它们的行列式的值分别为-2，0，-4。所以：

$det(A)=1\times (-2)-5\times 0 +0\times (-4)=-2$

而对于更高阶的行列式的计算，需要多次嵌套直到变成求二阶行列式。这似乎太麻烦了，有没有一种快捷一点的计算方式呢？

为了简洁，后面我们将使用$C_{ij}$来简化我们的表达：

$C_{ij}=(-1)^{i+j}\cdot det(A_{ij})$

准备工作

上面的行列式求和公式只是以第一行来计算。其实，这个公式可以选择任意一行$u$或者任意一列$u$来表达，即：

$det(A)=\sum_{i=1}^{n}{a_{iu}\cdot\ C_{iu}}\\ det(A)=\sum_{i=1}^{n}{a_{ui}\cdot\ C_{ui}}$

所以无论你以任意一行来计算，或者任意一列来计算，每一项的正负性都是交替的：

$\left [ \begin{matrix} +&-&+&\cdots\\ -&+&-&\\ +&-&+&\\ \vdots&&&\ddots \end{matrix} \right ]$

既然我们可以从任意一行或者一列来算，我们回到上面的三阶行列式，可以发现第三行有两个0：

$\left | \begin{matrix} 1&5&0\\ 2&4&-1\\ 0&-2&0 \end{matrix} \right |$

我们用第三行来算：

$det(A)=a_{31}\cdot C_{31}-a_{32}\cdot C_{32}+a_{33}\cdot C_{33}$

会发现$a_{31}$和$a_{33}$都是0，那么我们只用算$-a_{32}\cdot C_{32}$一项就能完成我们的运算了，计算出来发现答案也是-2，准确无误！

行变换与行列式

既然这样，那能不能将这个矩阵像高斯消元一样，用行变换将最后一行除了最后一项全都是0呢？那时我们用最后一行来计算，工作量就能只剩一项了。

答案是可以！

加加减减

首先，对行进行加减操作，不会影响行列式的值。

为什么这样讲呢？我们学过，对于平行四边形的面积，底面不变、高不变的情况下，可以把顶点沿着底面的平行线方向任意移动而不会改变面积。不如我们举个例子：

$a=\left[\begin{matrix}2\\1\\\end{matrix}\right] b=\left[\begin{matrix}1\\3\\\end{matrix}\right]$

然后，将向量$a$的$-\frac{1}{2}$倍加到向量$b$上，在图像上就是将蓝色面积向左拉到了$y$轴，变成了绿色面积：

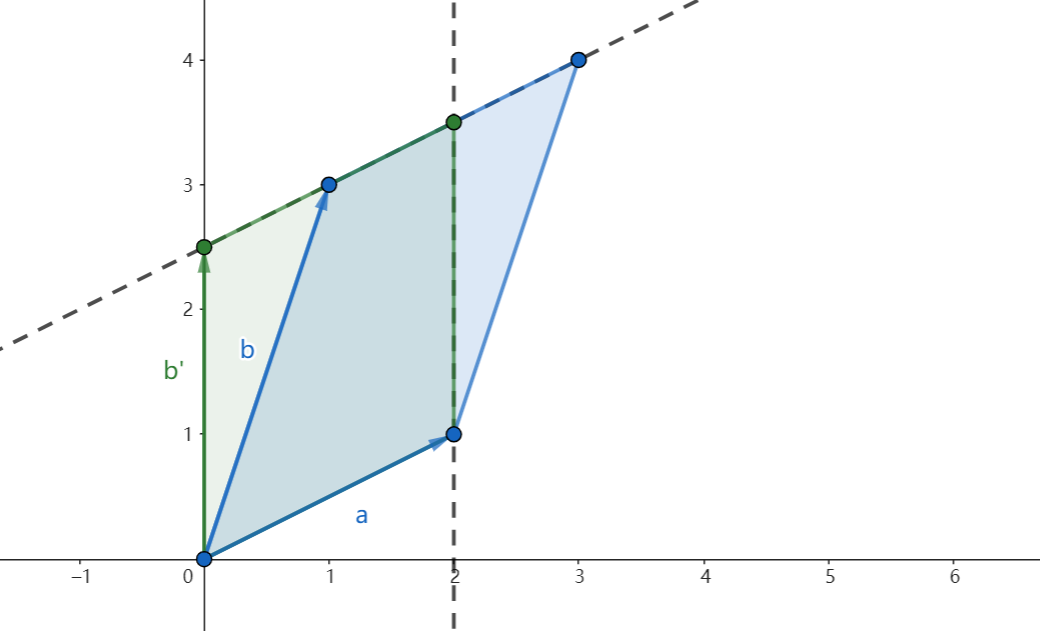
然后，我们将向量b的$-\frac{2}{5}$倍加到向量a上，就是将绿色面积向下拉成了橘色面积：

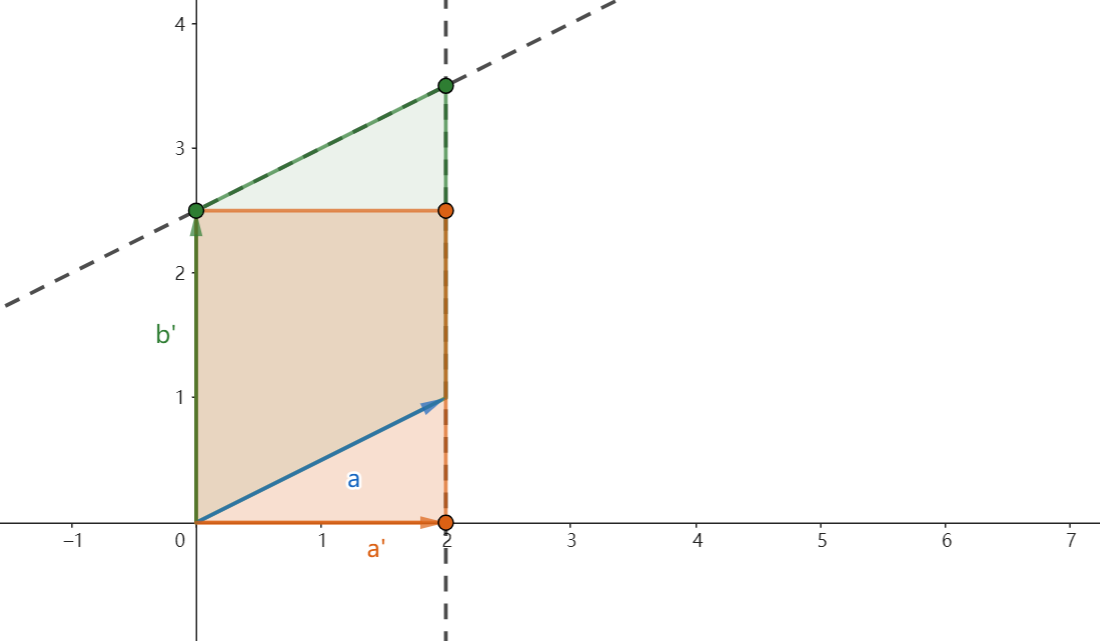
所以，加减的行变换相当于是把图像拉直靠近坐标轴，方便我们运算，不会改变结果。

提出来！

行列式中的行或者列而已把相同的倍数提出来~这个很好理解吧，就是这样：

$\left|\begin{matrix}2&4\\1&1\\\end{matrix}\right| = 2\left|\begin{matrix}1&2\\1&1\\\end{matrix}\right|$

交换顺序

在行列式中两行交换，会让结果变号：

$\left|\begin{matrix}2&-4\\3&1\\\end{matrix}\right| = -\left|\begin{matrix}-2&4\\3&1\\\end{matrix}\right|$

为什么会这样？因为行数或者列数的交换，打乱了我们行列式计算中$(-1)^{i+j}$的正负性。

更加具象得说，就是将空间内的坐标轴进行了对调，导致了空间的翻面，所以改变了正负。